Math Cheat Sheet for Trigonometry This website uses cookies to ensure you get the best experienceRecall the following identities $$\sin(2 \theta) = 2 \sin(\theta) \cos(\theta)$$ $$1\cos(2 \phi) = 2 \sin^2(\phi)$$ Make use of the above identities and you will get your solution Move your cursor over the gray area for complete solutionStart studying trig identities and log rules Learn vocabulary, terms, and more with flashcards, games, and other study tools
Bestmaths Online Proof 4
Trig identities tan^2x
Trig identities tan^2x-To integrate tan^22x, also written as ∫tan 2 2x dx, tan squared 2x, (tan2x)^2, and tan^2(2x), we start by utilising standard trig identities to change the form of the integral Our goal is to have sec 2 2x in the new form because there is a standard integration solution for that in formula booklets that we can use We recall the Pythagorean trig identity, and multiply the angles by 2Trig Cheat Sheet Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p




Trig Identities Assignment Math Forums
Here I give proofs of two Pythagorean trigonometric identities you should knowsin divided by cos equals tan and sin squared plus cos squared equals 1YOUTUBProve the following trig identities a) manipulate left side factorProve\\tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) prove\\cot(2x)=\frac{1\tan^2(x)}{2\tan(x)} prove\\csc(2x)=\frac{\sec(x)}{2\sin(x)} prove\\frac{\sin(3x)\sin(7x)}{\cos(3x)\cos(7x)}=\cot(2x) prove\\frac{\csc(\theta)\cot(\theta)}{\tan(\theta)\sin(\theta)}=\cot(\theta)\csc(\theta) prove\\cot(x)\tan(x)=\sec(x)\csc(x)
For more resources, visit http//wwwblackpenredpencomTrigverifying trigonometric identities, full playlist https//wwwyoutubecom/playlist?list=PLj7p5OIn this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometricCos^2 x = 1 cos (2x) / 2 power reducing Identity tan^2 x 1 cos (2x) / 1 cos (2x) half angle formula for sine sin (x/2) = / square root of ( 1cosx ) / 2 half angle formula for cosine cos (x/2) = / square root of ( 1 cosx ) / 2 half angle formula for tangent
Various identities and properties essential in trigonometry Legend x and y are independent variables, d is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x /cos x equation 1Sec^6x tan^6x = 1 2 tan^2x sec^2x Important Difficult Trigonometric Identity Excellent application of Pythagorean Trig Identities email anilanilkhandelwal@gmailcomProof of The Pythagorean trigonometric identity To prove that s i n 2 ( x) c o s 2 ( x) = 1 we can start by drawing a right triangle From the pythagorean theorem we know that a 2 b 2 = c 2 Now lets express a and b by using the sine and cosine 1) s i n v = b c b = c s i n v 2)



Ilectureonline



Determining Non Permissible Values In Trig Studypug
In mathematics, inverse trigonometric functions are also known as arcus functions or antitrigonometric functions The inverse trigonometric functions are the inverse functions of basic trigonometric functions, ie, sine, cosine, tangent, cosecant, secant, and cotangent It is used to find the angles with any trigonometric ratioCos 2x ≠ 2 cos x;Simplify trigonometric expressions Calculator online with solution and steps Detailed step by step solutions to your Simplify trigonometric expressions problems online with our math solver and calculator Solved exercises of Simplify trigonometric expressions



Answered Trigonometric Identities And Equations Bartleby
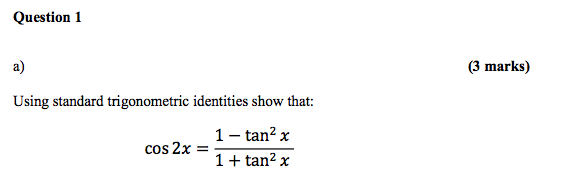



A Using Standard Trigonometric Identities Show That Chegg Com
Sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) cos x cos y = 2 sin ( (x y)/2 ) sin ( (x y)/2 ) Trig Table of Common Angles angleBasic Trig Identities The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variablesSo, these trig identities portray certain functions of at least one angle (it could be more angles) It is identified with a unit circle where the connection between the lines and angles in a Cartesian plane Proving trig identity $\tan(2x)−\tan(x)=\frac{\tan(x)}{\cos(2x)}$ Ask Question Asked 4 years, 1 month ago Active 4 years, 1 month ago Viewed 4k times 1 1 $\begingroup$ I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x




Trig Identities Assignment Math Forums




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic
The main trigonometric identities between trigonometric functions are proved, using mainly the geometry of the right triangle For greater and negative angles, see Trigonometric functions Elementary so the result follows from the triple tangent identityTrigonometric Identities mcTYtrigids091 In this unit we are going to look at trigonometric identities and how to use them to solve trigonometric equations In order to master the techniques explained here it is vital that you undertake plenty of practice exercises soTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube
Tan 2x ≠ 2 tan x by Shavana Gonzalez This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Confirming that the result is an identity Yes, sec2 − 1 = tan2x is an identity Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example \(Tan 2x =\frac{2tan x}{1tan^{2}x} \)




Analytic Trig Ppt Video Online Download




Using Trigonometric Identities Video Khan Academy
In this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometricStart studying Trig Identities Learn vocabulary, terms, and more with flashcards, games, and other study toolsFree trigonometric identities list trigonometric identities by request stepbystep This website uses cookies to ensure you get the best experience By



1




Trigonometry Reciprocal Identities Expii
The more important identities You don't have to know all the identities off the top of your head But these you should Defining relations for tangent, cotangent, secant, and cosecant in terms of sine and cosine The Pythagorean formula for sines and cosines This is probably the most important trig identityThe inverse trigonometric identities or functions are additionally known as arcus functions or identities Fundamentally, they are the trig reciprocal identities of following trigonometric functions Sin Cos Tan These trig identities are utilized in circumstances when the area of the domain area should be limited These trigonometry functions have extraordinary noteworthinessTherefore in mathematics as well as in physics, such formulae are useful for deriving many important identities The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is




Double Angle Trig Identities Quiz Quiz Quizizz




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
Trigonometry Identities STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by acopon1061 Terms in this set (21) sin 1/csc cos 1/sec tan 1/cot sin/cos csc 1/sin sec 1/cos cot 1/tan, cos/sin sin and cos identity sin^2xcos^2x=1 cot and csc identity 1cot^2x=csc^2x tan/sec identity tan^2x1=sec^2x sinThe trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functionsTRIGONOMETRIC IDENTITIES RECIPROCAL IDENTITIES PYTHAGOREAN = x SUM AND sin x sin tan ± y DOUBLEANGLE IDENTITIES 2x = 2 = = x — X — tan x tan = HAL F ANGLE sin tan




Trig Double Identities Trigonometric Double Angle Functions Trig




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
Trig identities or a trig substitution mcTYintusingtrig091 Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities These allow the integrand to be written in an alternative form which may be more amenable to integrationPDF Trigonometric identities are mathematical equations which are made up of functions These identities are true for any value of the variable put There are many identities which are derived by the basic functions, ie, sin, cos, tan, etc The most basic identity is the Pythagorean Identity, which is derived from the Pythagoras TheoremExplanation Following table gives the double angle identities which can be used while solving the equations You can also have sin2θ,cos2θ expressed in terms of tanθ as under sin2θ = 2tanθ 1 tan2θ cos2θ = 1 −tan2θ 1 tan2θ sankarankalyanam 1



Q Tbn And9gctg1mv4zqwzzx9es1vyuwisok4cikumrujuyo2nyqlvyw5qkqqv Usqp Cau
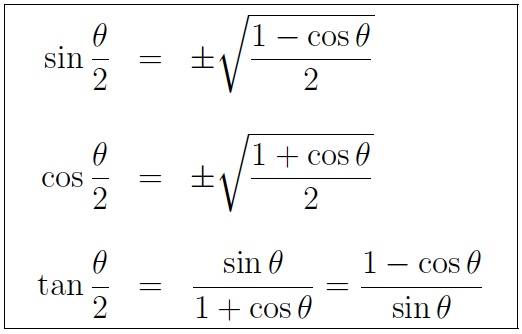



Trig Identities Table Of Trigonometric Identities
In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per Class 10, 11 and 12 syllabi Also, find the downloadable PDF of trigonometric formulas at BYJU'SBasically, If you want to simplify trig equations you want to simplify into the simplest way possible for example you can use the identities cos^2 x sin^2 x = 1 sin x/cos x = tan x You want to simplify an equation down so you can use one of the trig identities to• Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;
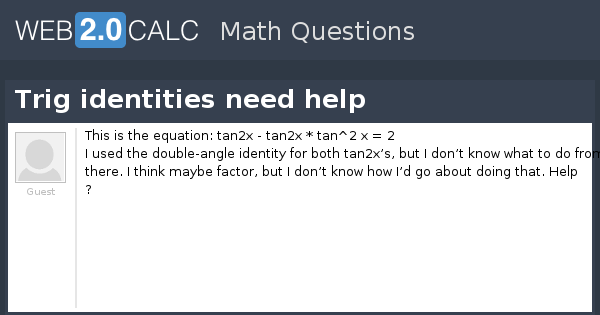



View Question Trig Identities Need Help



Precalc Wup 216 Using Trig Identities 2 Simplify
#=sin^2x/cos^2x# Reapplying the quotient identity, in reverse form #=tan^2x# b) Simplify #(cscbeta sin beta)/cscbeta# Apply the reciprocal identity #cscbeta = 1/sinbeta# #=(1/sinbeta sin beta)/(1/sinbeta)# Put the denominator on a common denominator #=(1/sinbeta sin^2beta/sinbeta)/(1/sinbeta)#Some common Identities and formulas generally used in finding Trigonometric ratios are stated below Double or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin TRIG Identities, Gr 12 Prove cot4x=1tan^2x/2tan2x Math Multiply then use fundamental identities to simplify the expression below and determine which of the following is not equivalent (2 2cos x)(2 2cos x) a4 4cos^2 x b 4 cos^2 x c4/(1 cot^2 x) d 4sin^2 x e4/(csc^2 x)




Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube
Question Prove the following trig identities a) tan 2x 2tan 2x sin^2x= sin 2 x b) sec^2x2sec x cos x cos^2x= tan^2x sin^2 x Answer by MathLover1 () ( Show Source ) You can put this solution on YOUR website!Trigonometricidentitycalculator Prove (sec^{4}x sec^{2}x) = (tan^{4}x tan^{2}x) en




Using Standard Trigonometric Identities Show That Chegg Com




Trig Identity Sec2x Minus Tan2x T10 Youtube
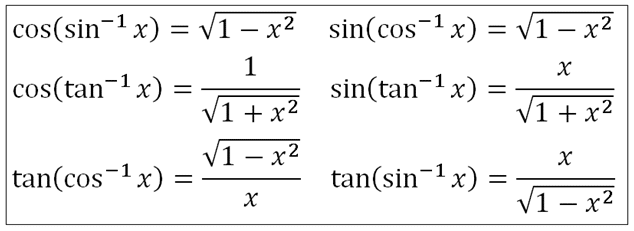



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig



What Is The Formula Of Tan2x Quora




Tan 2x Formula What Is Tan 2x Formula Examples




Integrate Sec 2x Method 2




2 Prove The Following Trig Identities A Prove Tan Chegg Com



6 1 2 Trigonometric Identities




Powers Of Trigonometric Functions




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube



Biomath Trigonometric Functions




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf




List Of Trigonometric Identities Wikipedia



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download




Trig Identities Maple Learn Maplesoft




Understanding Pythagorean Identities Studypug



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Solving Trigonometric Equations Ck 12 Foundation




Reciprocal Identities In Trigonometry With Examples Owlcation




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X 1 Ppt Powerpoint



Bestmaths Online Proof 4




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



How Do You Simplify The Identify Sin 2x 1 Cosx 1 Cosx Socratic




How To Use Trig Identities Mathematics Stack Exchange



1



7 Proving Ids Trig Functions Identities




Tangent Half Angle Formula Wikipedia




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity
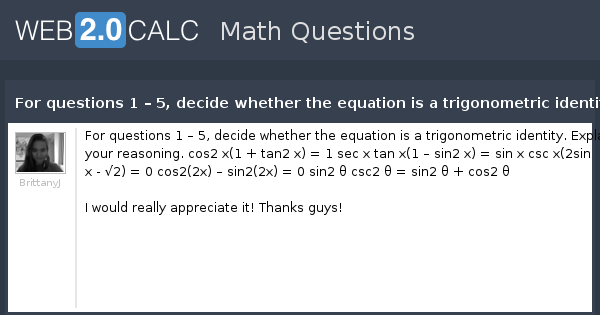



View Question For Questions 1 5 Decide Whether The Equation Is A Trigonometric Identity Explain Your Reasoning




Trig Identities Bingo Card



A Trig Identity
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




7 4 Proving Trigonometric Identities Mhf4utrigonometry



Trig Identities Hsn Forum



Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Analytic Math2412 Double Angle Power Reducing Half Angle Identities Pdf




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
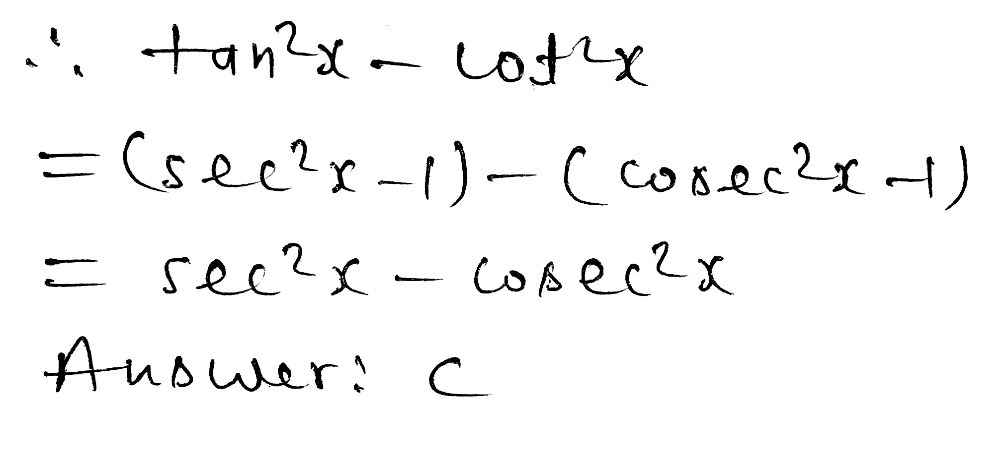



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath




Trig Identities And Formulas Pre Calculus Quiz Quizizz




Chapter 11 Trigonometric Identities And Equations 11 1




Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre



3



Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com



Mrsmkramer Weebly Com Uploads 3 5 9 0 Trig Cheat Sheet Pdf



What Is The Formula Of Tan2x Quora
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com



Biomath Trigonometric Functions




2 Prove The Following Trig Identities A Prove Tan Chegg Com




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf



What Are The Quotient Identities For A Trigonometric Functions Socratic
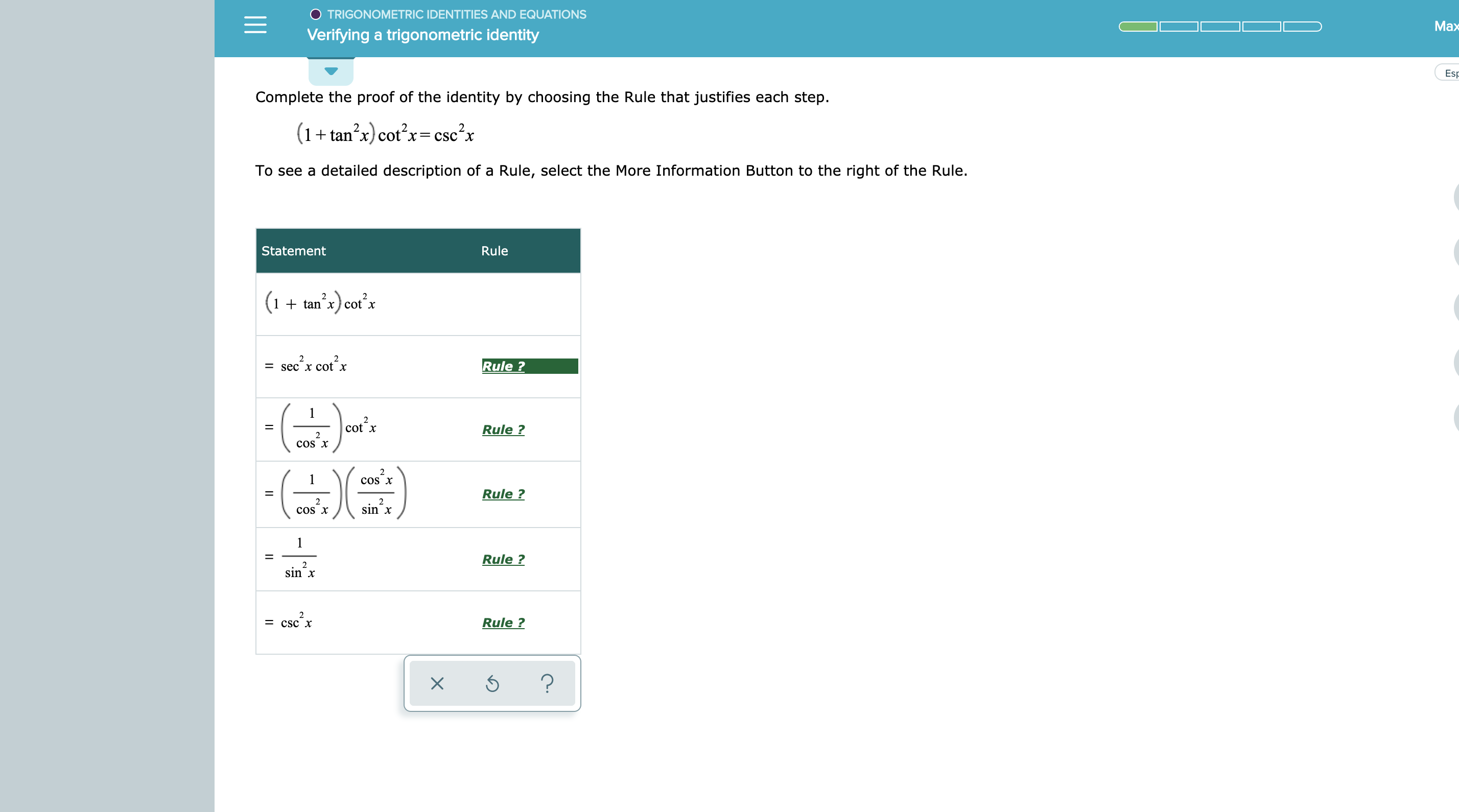



Answered Trigonometric Identities And Equations Bartleby
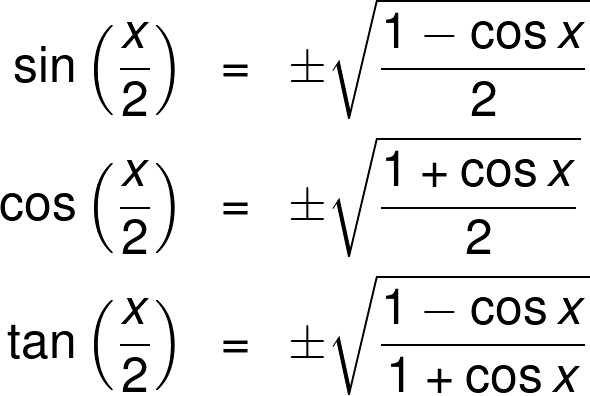



Half Angle Calculator




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube



Solved Prove The Following Trig Identities Course Hero




Trig Identities Table Of Trigonometric Identities




Ppt Basic Trig Identities Sin 2 X Cos 2 X 1 Powerpoint Presentation Id




Sum And Difference Identities Video Lessons Examples And Solutions




Integrate Sec 2x Method 1




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube




Chapter 5 Trigonometric Identities Review Sheet



F4ntussz Z2tvm




Alternate Forms Of Trigonometric Identities Video Lesson Transcript Study Com



Trig Identities Hsn Forum




Trigonometric Identities And Examples With Worksheets




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Simplify Each Of The Following Trigonometric Chegg Com




Trig Identities Bingo Card




9 1 Identities And Proofs Ppt Download




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi




Trigonometric Identities Trigonometric Functions Trigonometry




2 Prove The Following Trig Identities A Prove Tan Chegg Com




Which Of The Following Expressions Completes The Identity 1 Sec 2 X Mathematics Stack Exchange



Derivatives Of Trigonometric Functions



Trig Identities Crossword Wordmint
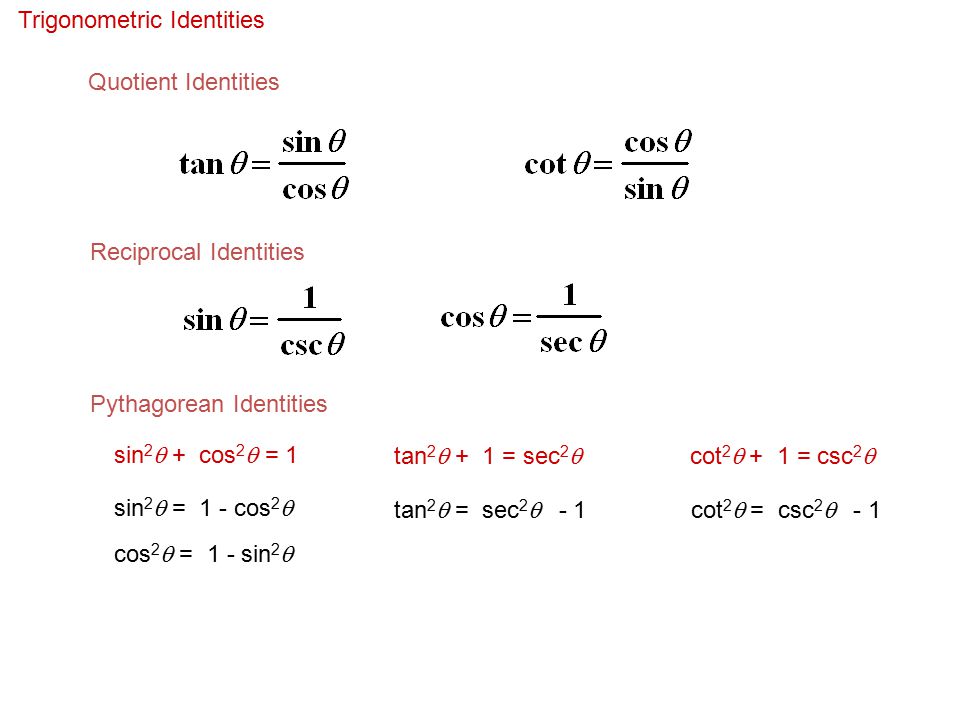



11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf



0 件のコメント:
コメントを投稿