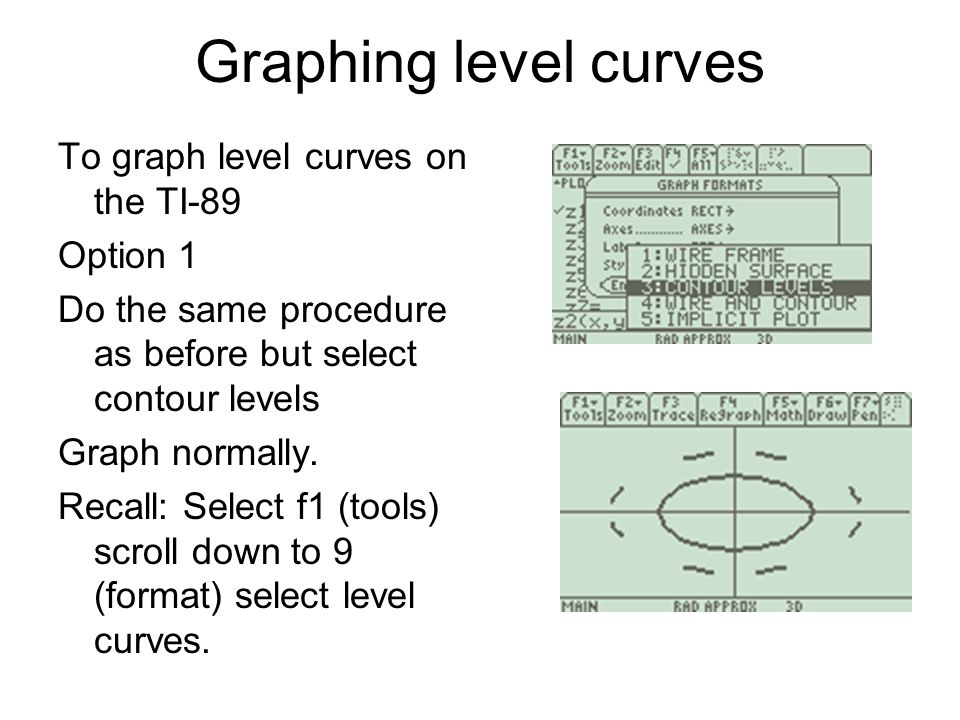
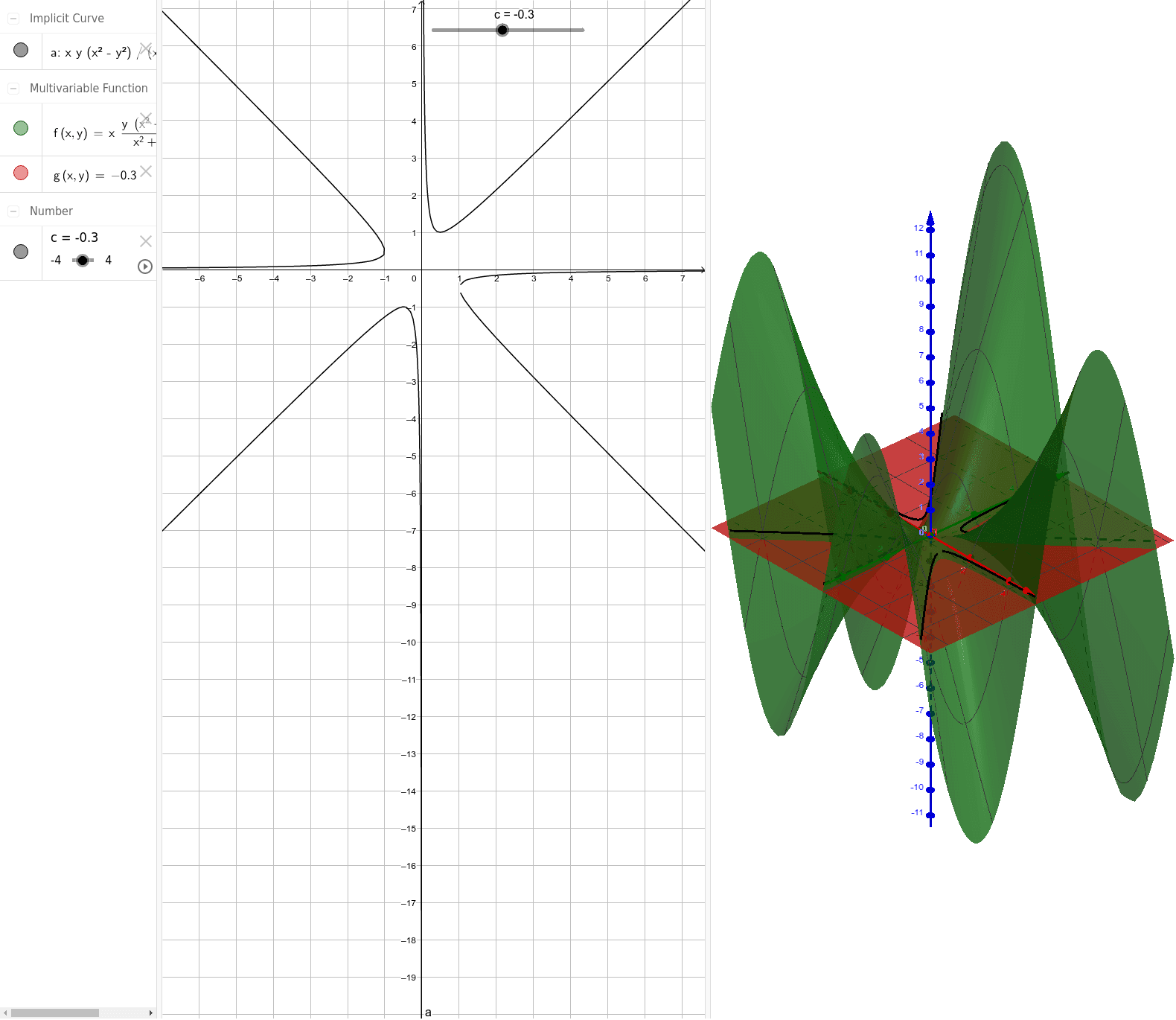
Add to graph Function z=f(x,y) Space Curve r(t) Vector Field Point (x, y, z) Vector Text Label Implicit Surface Parametric Surface Region Slider ────────── Function r=f(θ,z) Function z=f(r,θ) Function ρ=f(θ,φ) Function x=f(y,z) Function y=f(x,z) Surface of RevolutionCurves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean \The I have the following code below, but I cannot test it since I do not have Matlab with me right now and I am afraid I might not have the time to test it by myself when I finally get it I'm trying to plot both 3d graphs and graphs of the level curves in the y and x axis (two dimensions only) of three different types of functions

Graphs And Level Curves
Level curve grapher online
Level curve grapher online-New url for the 3D plotter https//wwwmonroeccedu/faculty/paulseeburger/calcnsf/CalcPlot3D/This video explains how to graph contour plots for functions oShare a link to this widget More Embed this widget » Added by RicardoHdez in Mathematics The level curves of f (x,y) are curves in the xyplane along which f has a constant value Send feedback Visit WolframAlpha




Contour Plot An Overview Sciencedirect Topics
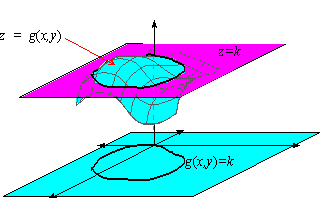
The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\)Free online 3D grapher from GeoGebra graph 3D functions, plot surfaces, construct solids and much more!A level curve of a function $f(x,y)$ is the curve of points $(x,y)$ where $f(x,y)$ is some constant value A level curve is simply a cross section of the graph of $z=f(x,y)$ taken at a constant value, say $z=c$ A function has many level curves, as one obtains a different level curve for each value of $c$ in the range of $f(x,y)$ We can plot the level curves for a bunch of different constants
In this video we're talking about how to sketch the level curves of a multivariable functionWhenever you're dealing with a multivariable function, the graphFree ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics andFree graphing calculator instantly graphs your math problems
Global Sea Levels Graph This graph features global sea level measurements from as far back as 800,000 years up to the present time with an atmospheric temperature overlay option The graph is customizable and can be resized, printed, or pasted into your website This is a free service, but we do ask for a donation if you find this usefulMath 210 is the third and the final part of our standard threesemester calculus sequence The distinct feature of this part of the course is its focus on the multidimensional analysis, as opposed to onedimensional analysis that students learned in Math 180 (Calculus I) and Math 181 (Calculus II) Math 210 focuses on important concepts suchThis graph shows the total number of tests done (gray bars), even if someone has been tested multiple times The test positivity rate (blue line) is the number of positive tests divided by the total number of tests done on a particular day The number of tests and test positivity are averaged over 7 days to smooth out the dips that occur when




Solved Sketch The Level Curves Of The Function Z F X Y 4aˆ X 2 Y 2




Graph And Contour Plots Of Functions Of Two Variables Wolfram Demonstrations Project
How to plot level curves of f(x,y) = 2x^2 Learn more about level curves, 3d plots, graphing• The level curves of a multivariate function are the lines for various values of the dependent variable f • Drawing level curves is a technique for graphing threedimensional surfaces • The directions of steepest ascent and descent are perpendicular to the level curves • Directions that are parallel to level curves are where theDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f



Level Curves And Contour Plots Mathonline



13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned
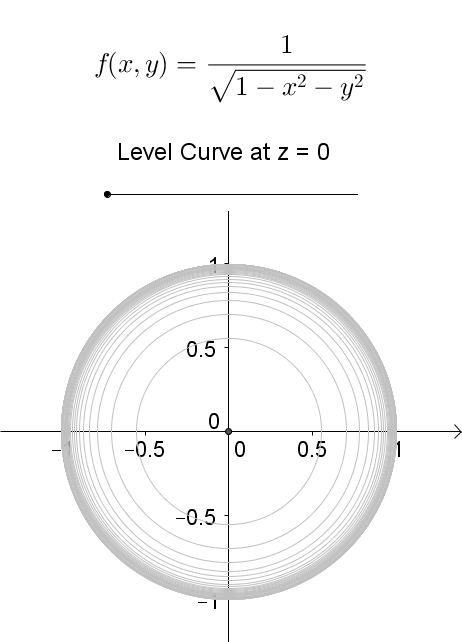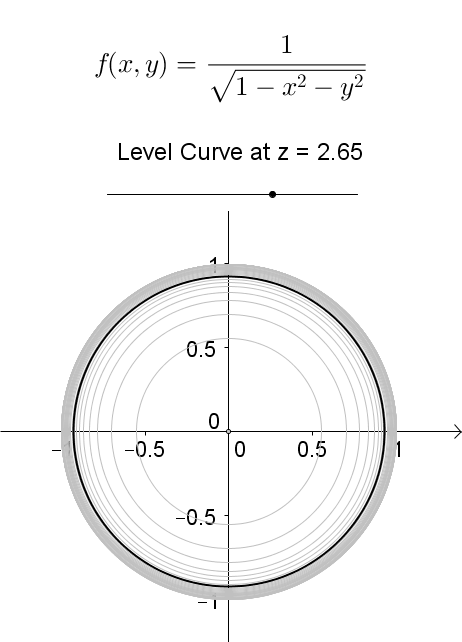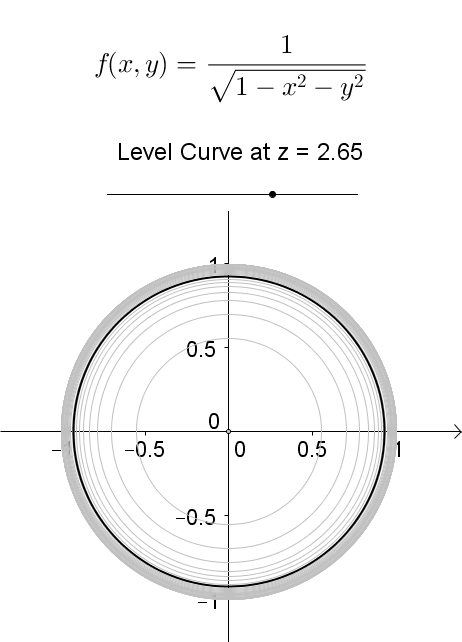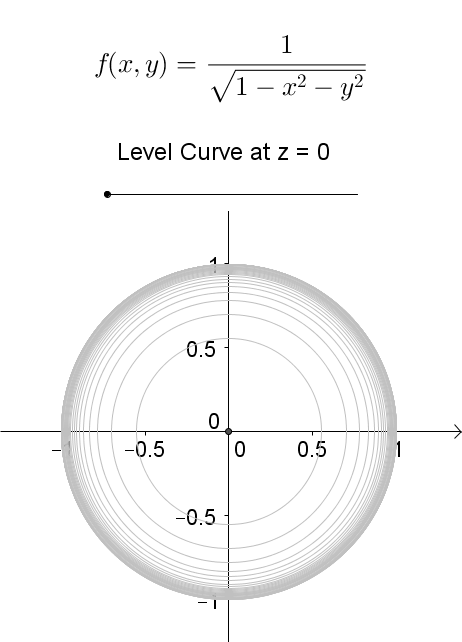
Figure \(\PageIndex{7}\) is a graph of the level curves of this function corresponding to \(c=0,1,2,\) and \(3\) Note that in the previous derivation it may be possible that we introduced extra solutions by squaring both sides This is not the case here because the range of the square root function is nonnegative calculus Graphing Level Curves Mathematics Stack Exchange 1 I'm not too sure how to go about doing questions like these This is from the text and I wanted to know the steps I take when doing level curve questions like the ones attached Specifically question 31Level curves Scroll down to the bottom to view the interactive graph A level curve of f ( x, y) is a curve on the domain that satisfies f ( x, y) = k It can be viewed as the intersection of the surface z = f ( x, y) and the horizontal plane z = k projected onto the domain The following diagrams shows how the level curves f ( x, y) = 1 1 − x 2 − y 2 = k
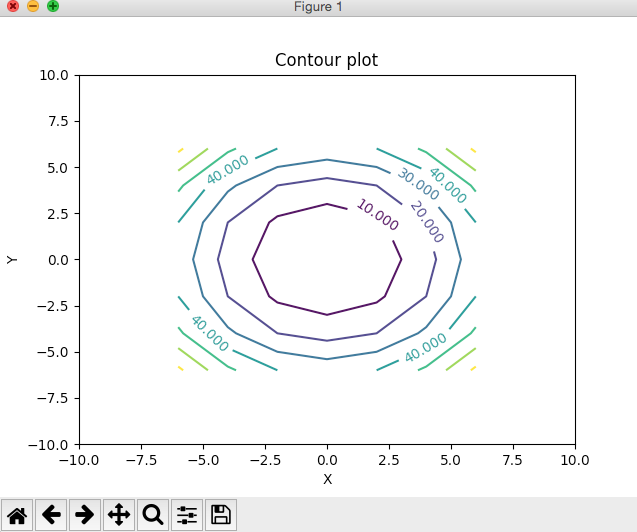



Contour Plot Using Python And Matplotlib Pythontic Com
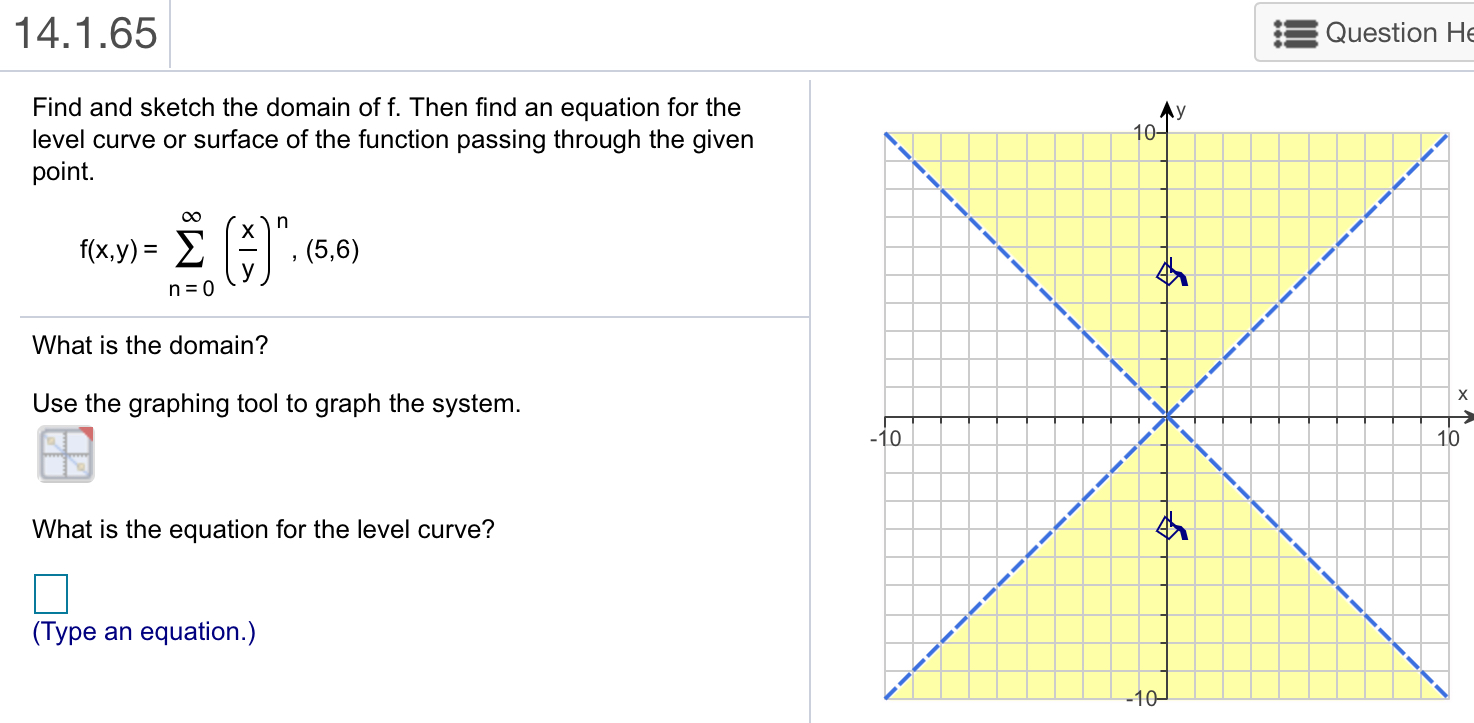



I Know That There Is Already A Chegg Question On Chegg Com
Mathematica has a builtin command to generate plots of the level curves of a function f of two variables The basic form of the command is where F x, y is an expression in the variables x and y, which range over the respective intervals xmin, xmax and ymin, ymax For the function f with formula f (x, y) = , with x and y eachSketch some level curves of the function Solution First, let z be equal to k, to get f(x,y) = k Secondly, we get the level curves, or Notice that for k>0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves ofLevel Curves Author Kristen Beck Topic Functions This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both and
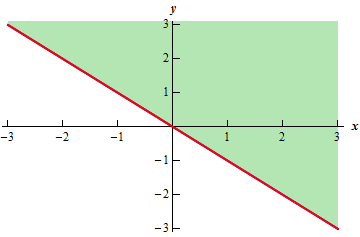



Calculus Iii Functions Of Several Variables
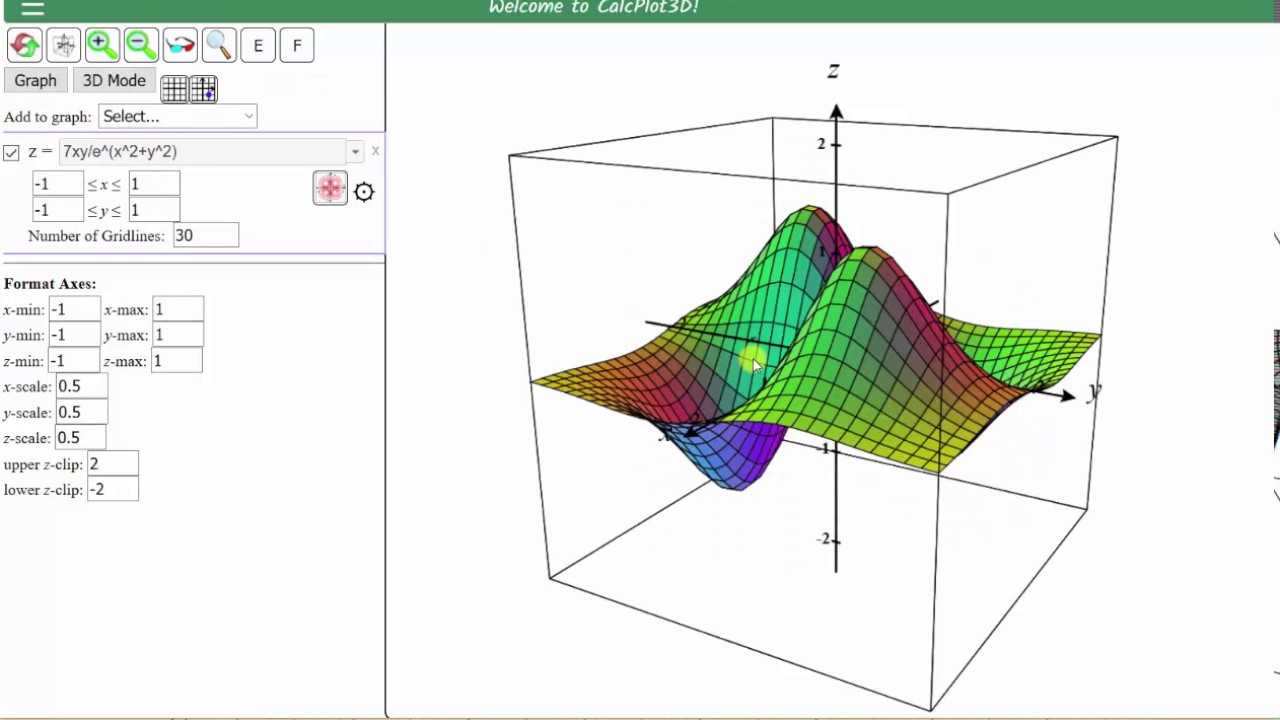



Graph A Contour Plots Level Curves Using 3d Calc Plotter Youtube
I am having a really hard time graphing or drawing level curves anything would help multivariablecalculus graphingfunctions Share Cite Follow asked Apr 15 '12 at 2140 Raynos Raynos 1,475 9 9 gold badges 29 29 silver badges 55 55 bronze badges $\endgroup$ Add a comment5 Plot the level curves by adding a 2D Graph page to the document and plotting the lists as f1(x)and f2(x) Modify the colors of the level curves if desired The examples use the color green for positive values of z, blue for z = 0, and orange for negative values of z 6 Use the Settings Settings dialog to hide the plot labels 7A free graphing calculator graph function, examine intersection points, find maximum and minimum and much more This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy




Level Curves Of Functions Of Two Variables Youtube




Calculus Iii Functions Of Several Variables
Level Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of cIf you are not satis ed by the number of level curves produced, it is a simple matter to add more The following command should produce 10 level curves, similar to those in Figure 4 >> contour(x,y,z,10) 22 Labeling the Contours It is a simple task to label each level curves with its constant function valueDesmos offers bestinclass calculators, digital math activities, and curriculum to help every student love math and love learning math



Contour Lines Rodolphe Vaillant S Homepage




Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube
The graph of the function f ( x, y) = − x 2 − 2 y 2 is shown is the first panel along with a level curve plot in the second panel The level curve f ( x, y) = c is shown in red in the level curve plot, which is the same as the slice of the graph z = f ( x, y) by the plane z = c You can change c by dragging the plane slicing the graph up orThe gov means it's official Municipal government websites often end in gov or org Before sharing sensitive information, make sure you're on a City of Chicago government siteLevel sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour of



Relief Functions And Level Curves



Www Arnoldfw Com Pdf Contour Plots Pdf
Visualizing level curves This allows students to see level curves drawn simultaneously with the 3D image of the intersection of the plane and the curve The only issue the user should be aware of is that the 2variable function must be polynomial in both x and y2 Answers2 Active Oldest Votes 1 In your first example, the proper solution is y = ± k − x 2 You left out the plusorminus That is not a small thing there are usually two values of y for each x, and that greatly affects the plotting of the curves I would say that there is no single general method for finding level curves, in a The level curves of f(x,y) = x 2y 2 are hyperbolas Here they are shown at the appropriate heights Example 7 The level curves of f(x,y)=2e(x1) 2y 2 3e(x2) 2(y1) 22e(x1) 2(y2) 2 are shown below Comparing with the graph in Example 4, we see that the points (x,y) at which f has maxima and minima are at the centers of circular level curves




Graphs And Level Curves
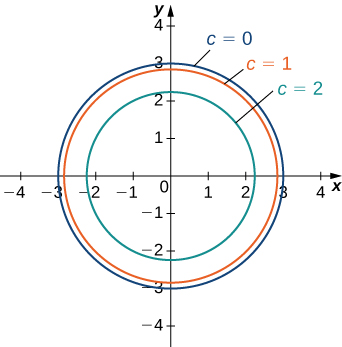



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize
Level surfaces For a function $w=f(x,\,y,\,z) \, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteqC Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 DGet the free "Plotting a single level curve" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha
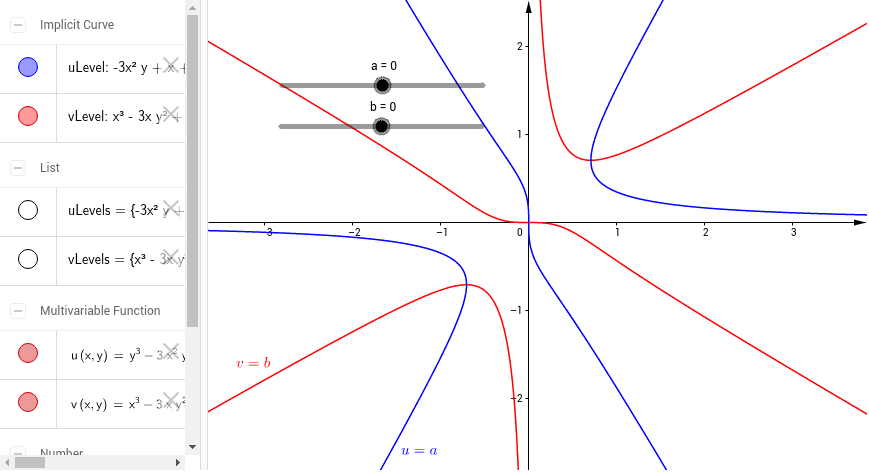



Level Curves Geogebra



Level Sets Ximera
Level Curve A level set in two dimensions Phase curves are sometimes also known as level curves (Tabor 19, p 14) SEE ALSO Contour Plot, Equipotential Curve, Level Surface, Phase Curve REFERENCES Tabor, M Chaos and Integrability in Nonlinear Dynamics An Introduction New York Wiley, 19So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming from So let's draw what's going on in three dimensionsMy Partial Derivatives course https//wwwkristakingmathcom/partialderivativescourseIn this video we're talking about how to sketch the level curves of



1
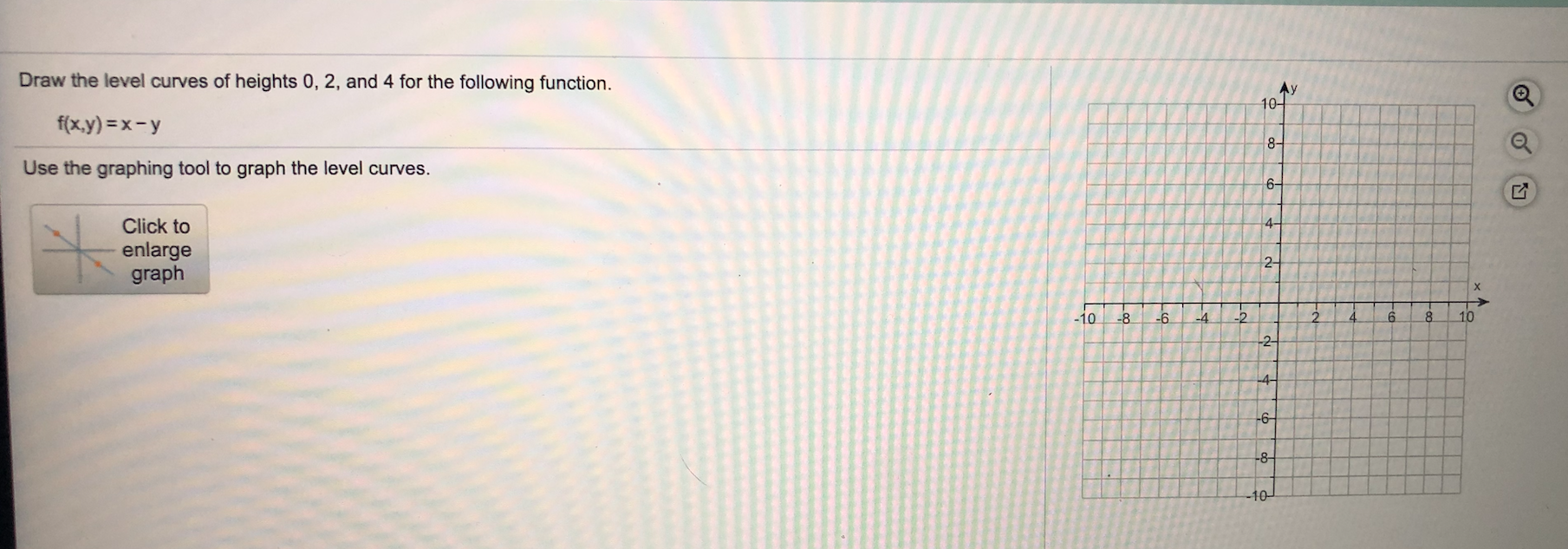



Draw The Level Curves Of Heights 0 2 And 4 For The Chegg Com
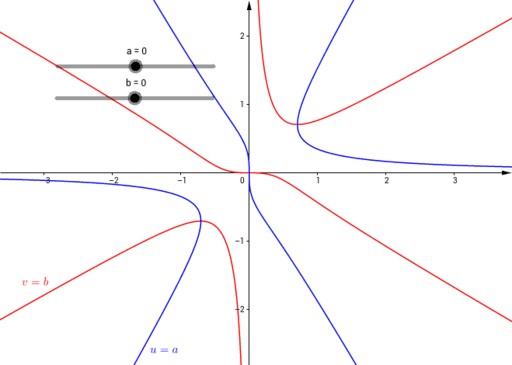
Level curves Author Siamak The level curves of two functions and Blue represents and red represents Since and are both harmonic and is a harmonic conjugate of , the level curves of and intersect each other at right anglesLet f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two linesLevel Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command plot3d For example, to plot the portion of the graph of the function f(x,y)=x 2 y 2 corresponding to x between 2 and 2 and y between 2 and 2, type > with (plots);




Gradients And Level Curves



Functions Of Several Variables Ximera
For each $c$, this is a line with slope $A/B$ and $y$intercept $y = (DCc)/B$ Since the slope does not depend on $c$, the level curves are parallel lines, and as $c$ runs over equally spaced values these lines will be a constant distance apart Consequently, the contour map of a plane consists of equally spaced parallel linesA collection of level curves of f is shown in the following figure The number on each curve is the value of the function to which it corresponds The circles are closer together for larger values of the function, so that the graph of the function is a bowl with sides whose slopes increase as we move away from the centerLevel Curves Level curves are slices through a surface When we have a surface z = f(x,y) z = f ( x, y) , level curves are horizontal slices of constant z z , ie they look like f(x,y) = k f ( x
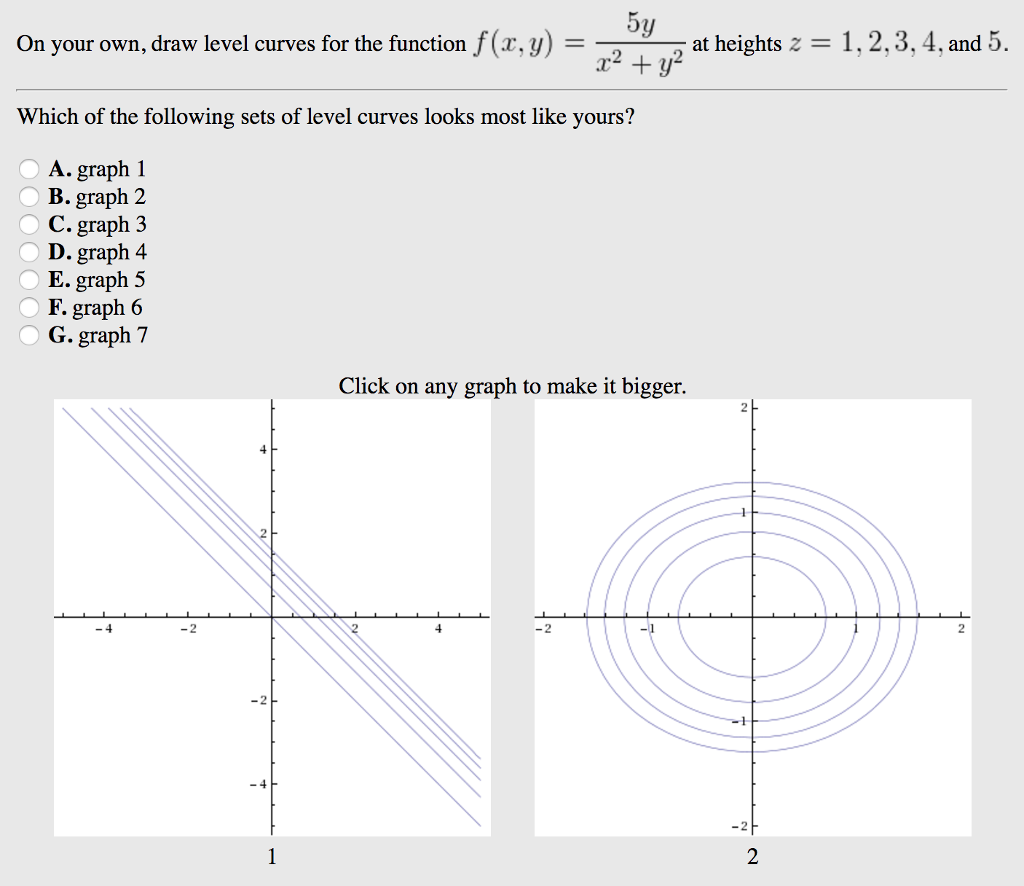



On Your Own Draw Level Curves For The Function F A Chegg Com




Graph A Contour Plots Level Curves Using 3d Calc Plotter Youtube
The level surface at I = c, where c > 0, is defined by c = 1 x 2 y 2 z 2 Algebra reveals \answer g i v e n x 2 y 2 z 2 = 1 c Given an intensity c, the level surface I = c is a sphere of radius 1 / c, centered at the origin Every point on each sphere experiences the same intensity of



Www Arnoldfw Com Pdf Contour Plots Pdf




Level Surfaces



Http Www Personal Psu Edu Sxj937 Math111 Lecture 11 Pdf




Level Curves For The Riemann Zeta Function Maths Paper Graphic Zeta




Level Sets Ximera




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
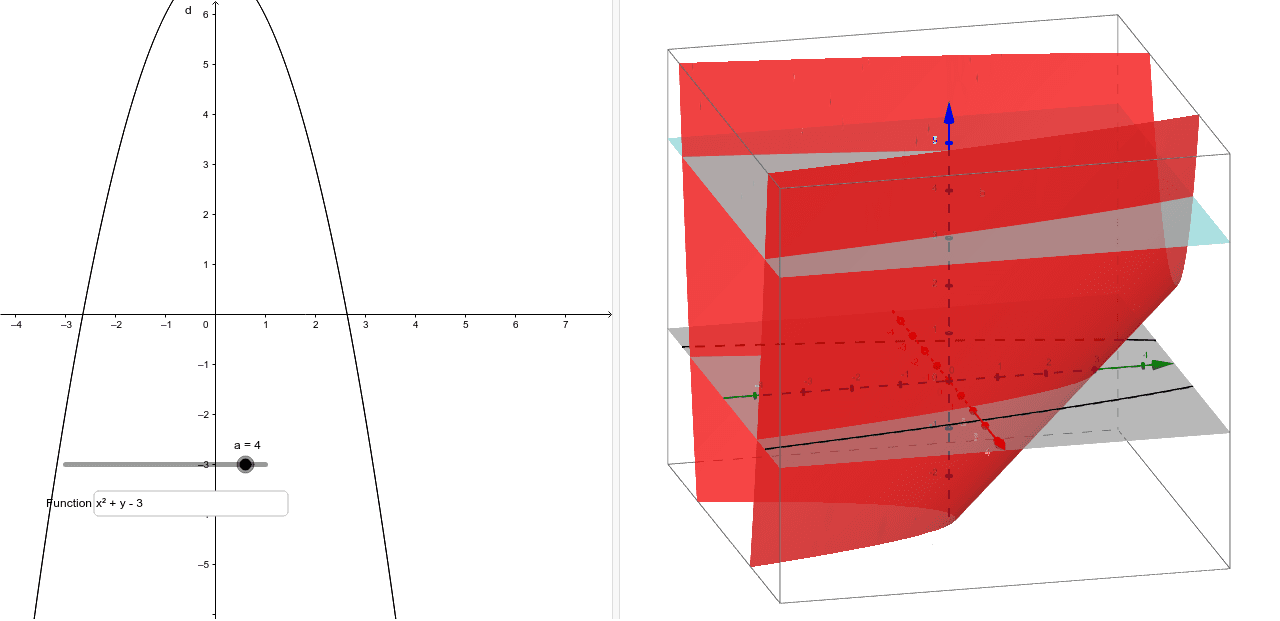



Visualizing Level Curves Geogebra




Level Set Wikipedia




How To Sketch Level Curves Youtube




14 1 Functions Of Several Variables Mathematics Libretexts
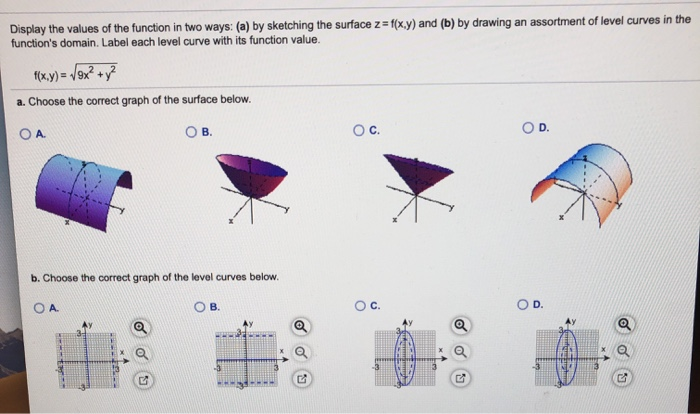



Display The Values Of The Function In Two Ways A Chegg Com




Contour Maps In Matlab




Contour Plot An Overview Sciencedirect Topics



If X X1 X2 Represents A Point In A Subset A Of Rn And F X Is Exactly One Point In Rm Then We Say That F



Level Curve Example Geogebra




Functions Of Several Variables




Level Surfaces



1
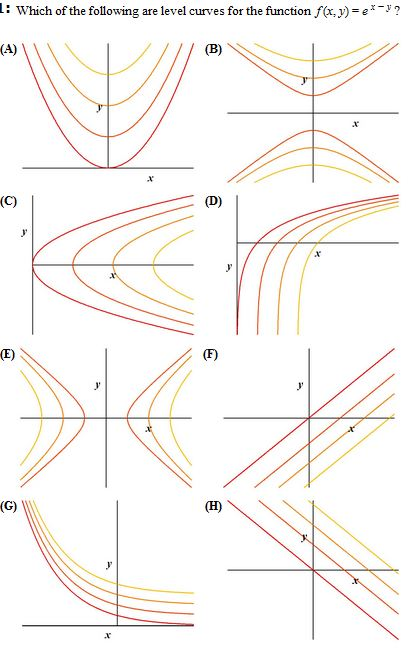



Which Of The Following Are Level Curves For The Chegg Com




Contourplot3d Maple Help




A Sketch The Gradient Vector Bigtriangledown F 4 6 For The Function F Whose Level Curves Are Shown Explain How You Chose The Direction And The Length Of This Vector B Find The Directional
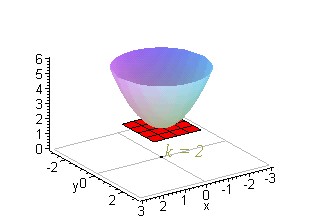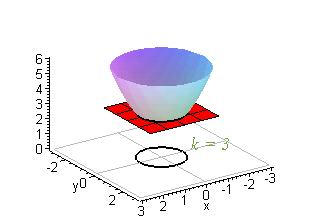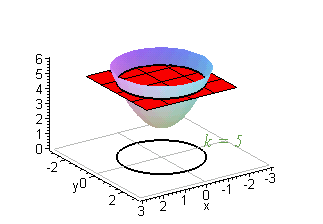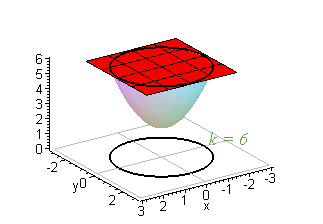



Gradients And Level Curves
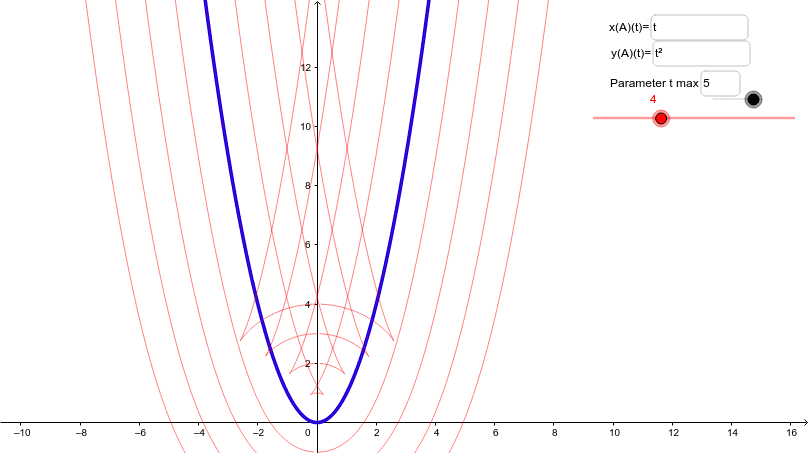



Level Curves Geogebra




Matlab Tutorial




Calculus Iii Functions Of Several Variables




Graphs And Level Curves



1




Level Set Examples Math Insight
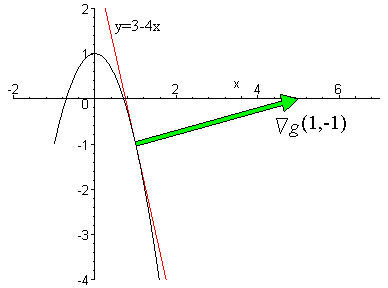



Gradients And Level Curves



Level Curves And Contour Plots Mathonline



Level Curves Geogebra




Level Curves



Gradients And Level Curves




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Level Curves Geogebra



Relief Functions And Level Curves



Level Curves




Based On The Level Curves That Are Visible In The Following Graph Identify The Approximate Locations Of The Local Homeworklib



Level Curves And Contour Plots Mathonline




16 1 Functions Of Several Variables




Visualizing Gradient Vectors With Level Curves Youtube
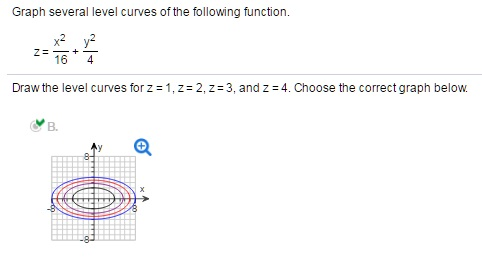



Graph Several Level Curves Of The Following Function Chegg Com
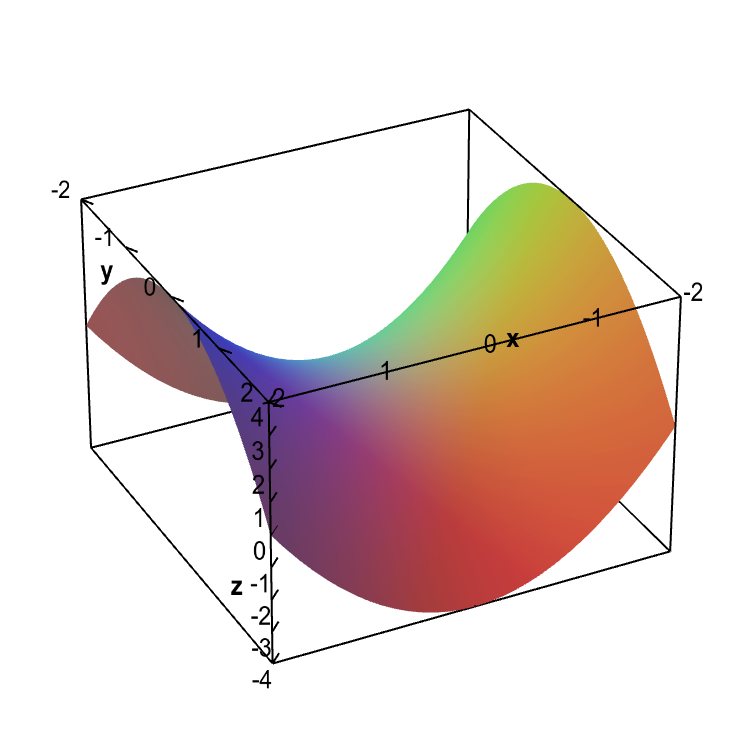



Level Set Examples Math Insight




Level Sets Math Insight




How Do You Plot Level Curves Describing A 3d Surface On The X Y Plane Mathematica Stack Exchange



1
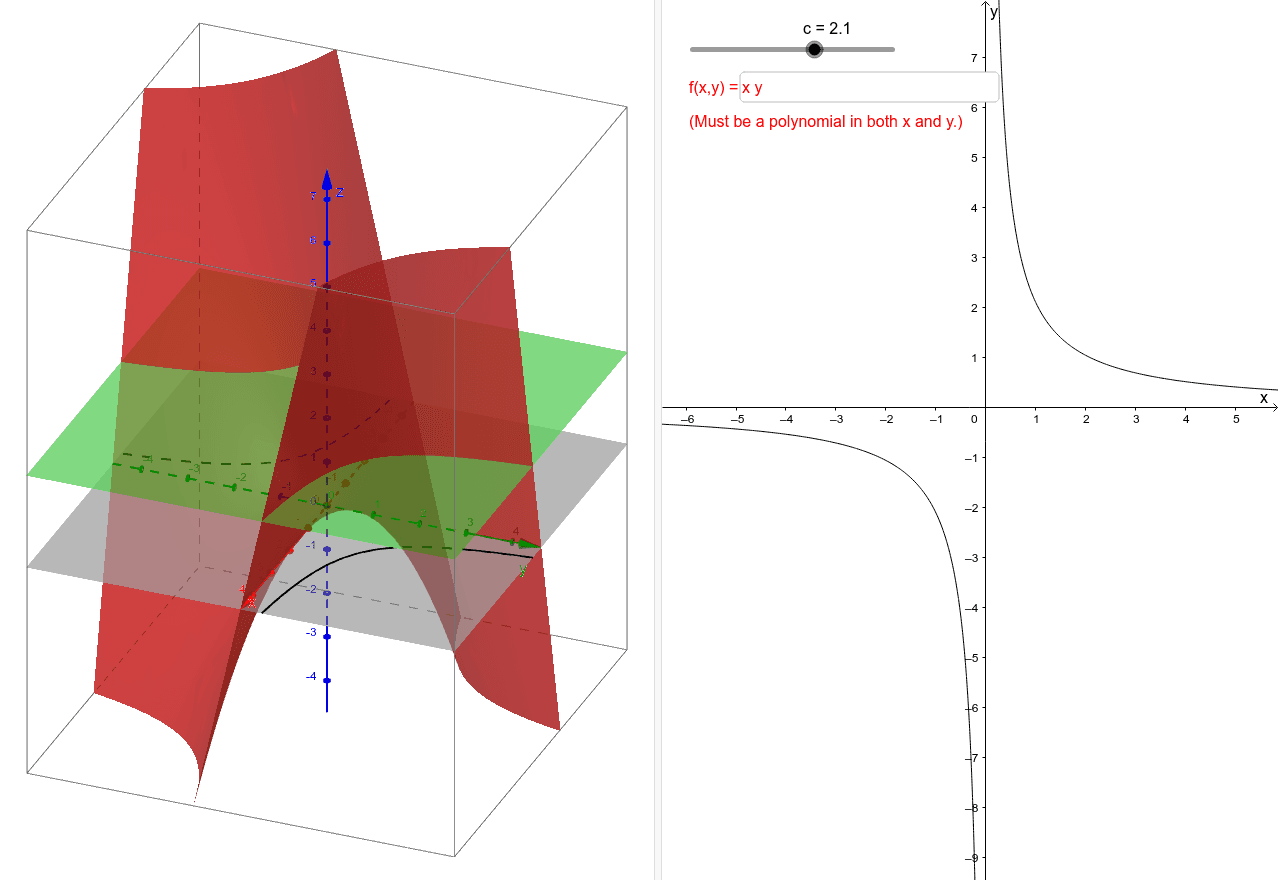



Level Curves Geogebra



Level Curves Geogebra Dynamic Worksheet




Level Set Wikipedia




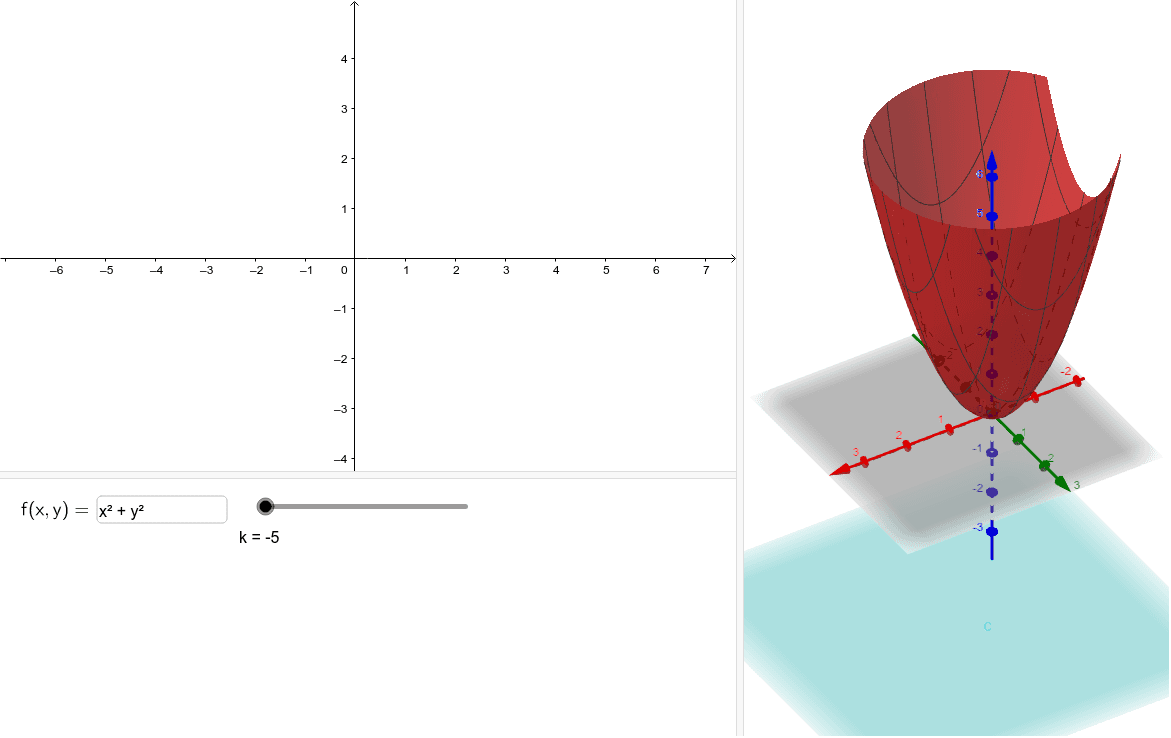
Solved Sketch The Level Curve Z K For The Specified Values Z X 2 Y 2 K 0 1 2 3 4
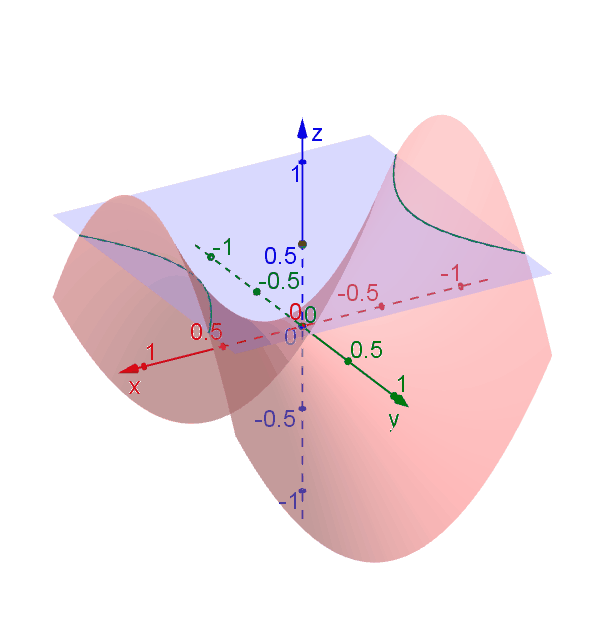



Hyperbolic Paraboloid Geogebra Dynamic Worksheet




Graphs And Level Curves




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
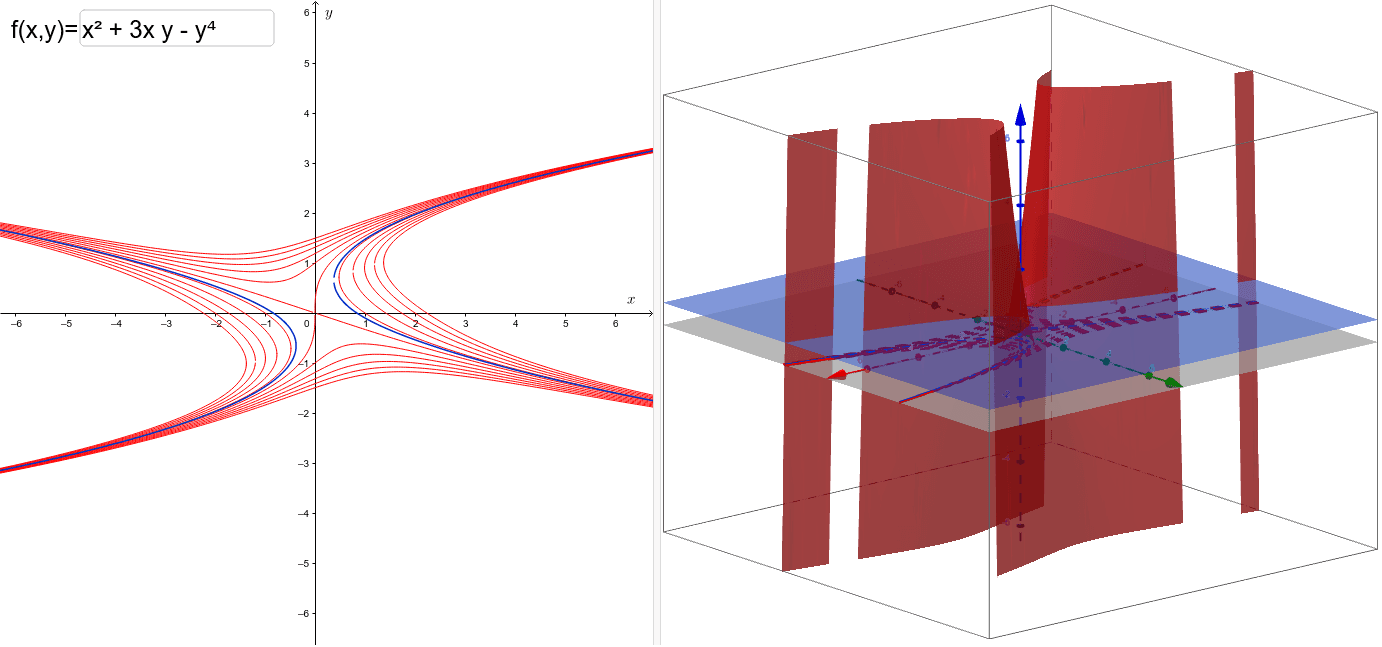



Level Curves Geogebra




Graphs And Level Curves
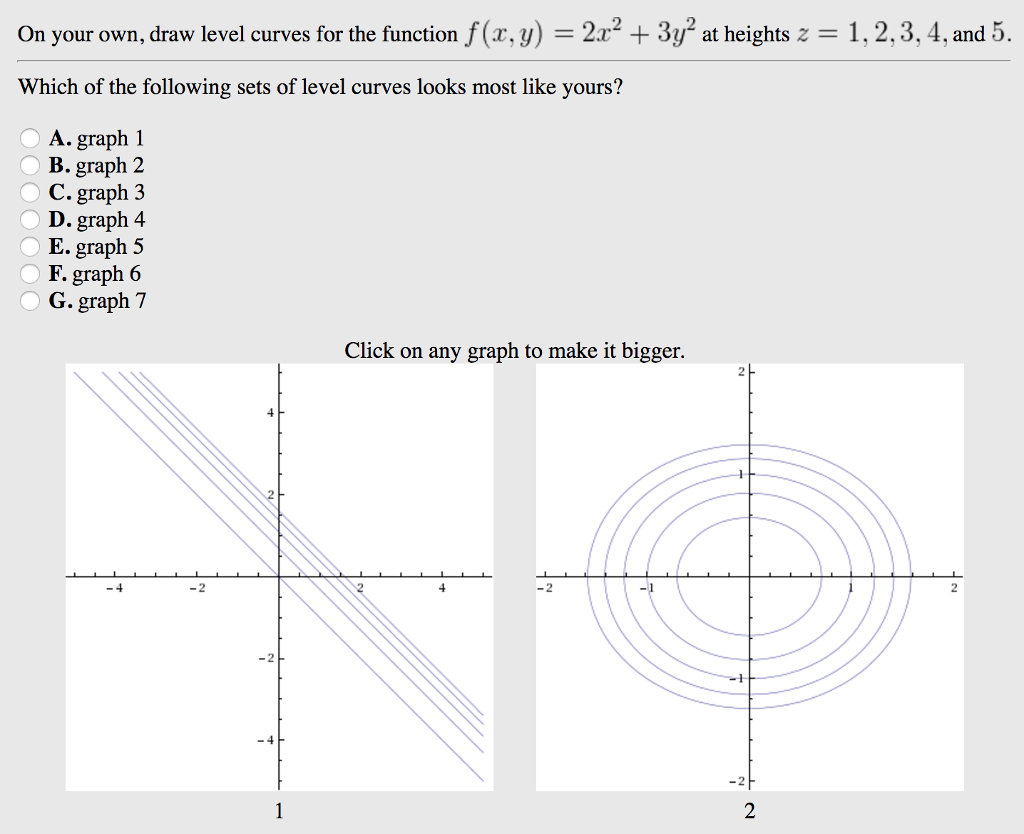



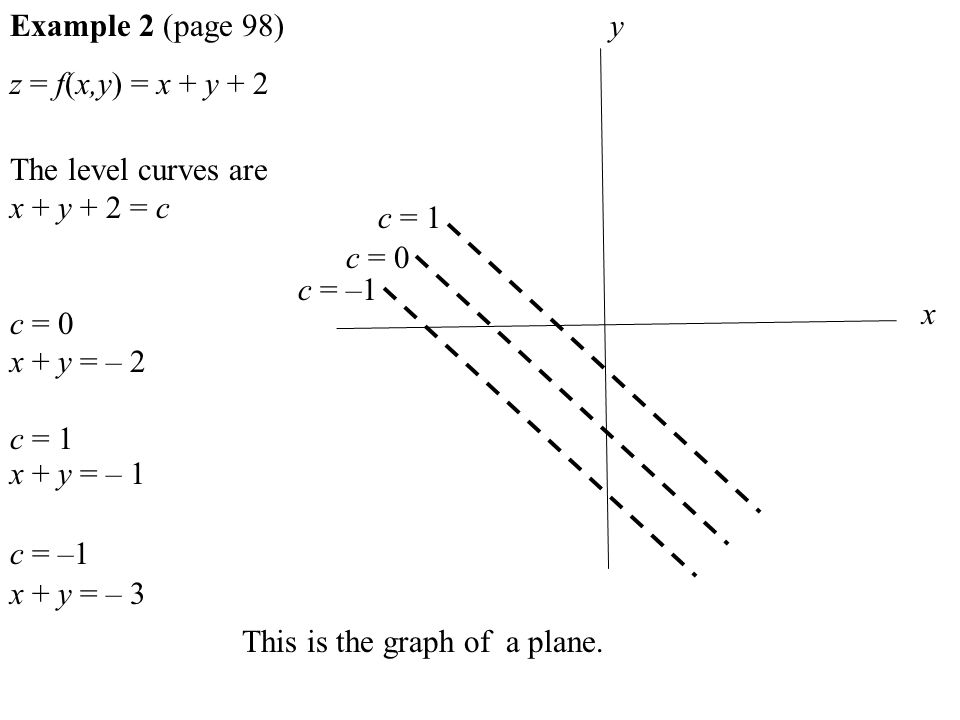
On Your Own Draw Level Curves For The Function F Z Chegg Com




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube



Level Sets Ximera




Level Curves




Calculus Iii Functions Of Several Variables




Level Curves Examples Level Surface




Graphing Level Curves Mathematics Stack Exchange




Orthogonality Of Level Curves Of Harmonic Conjugates An Example Of 3rd Degree Geogebra
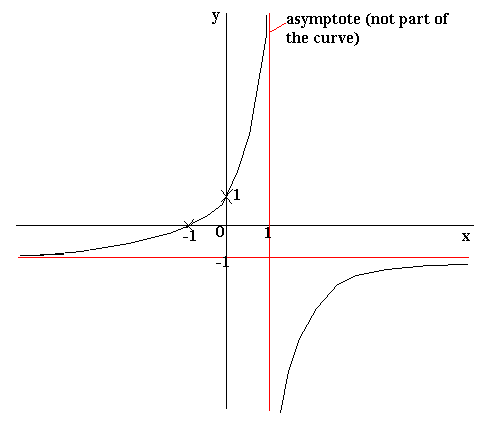



Curve Sketching Mathematics A Level Revision




Matlab Tutorial




Level Sets Math Insight




Level Set Wikipedia
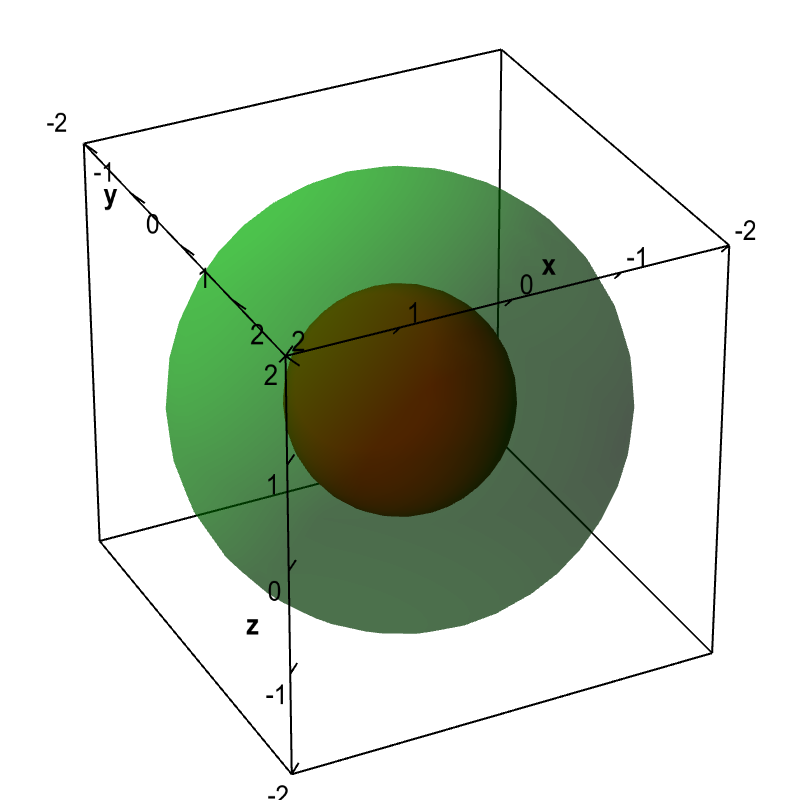



Level Set Examples Math Insight




A Use The Level Curves In The Figure To Predict The Chegg Com




Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com



Business Calculus



Level Curves




Functions Of Several Variables Ppt Download




Level Curves Of Function At Z 0 Mathematics Stack Exchange
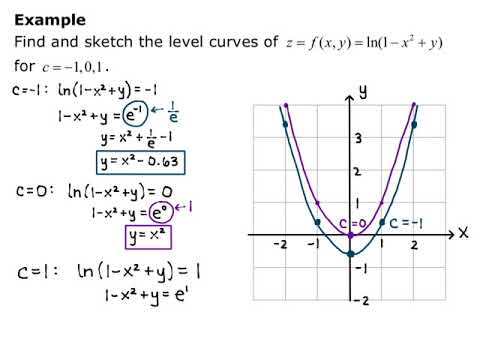



Section 13 1 Level Curves Youtube




Graph The Level Curves Of F X Y Frac Y K For K 1 2 4 Study Com
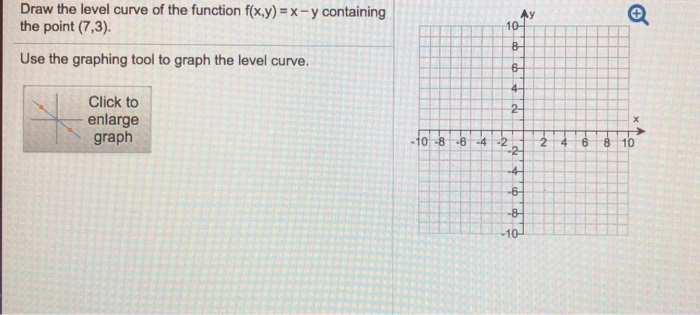



Draw The Level Curve Of The Function F X Y X Y Chegg Com




Level Curves




Level Set Examples Math Insight




Applet Level Curves Of An Elliptic Paraboloid Shown With Graph Math Insight



0 件のコメント:
コメントを投稿